In state-of-the-art DFT algorithms a sizeable number of computational parameters, such as damping, mixing/preconditioning strategy or acceleration methods, need to be chosen. This is usually done empirically, which bears the risk to choose parameters too conservatively leading to sub-optimal performance or too optimistically leading to limited reliability for challenging systems.
Our recent work along this research direction has resulted in a number of improved algorithms for density-functional theory (DFT) by combining insights from numerical analysis with physical principles [1][2][3].
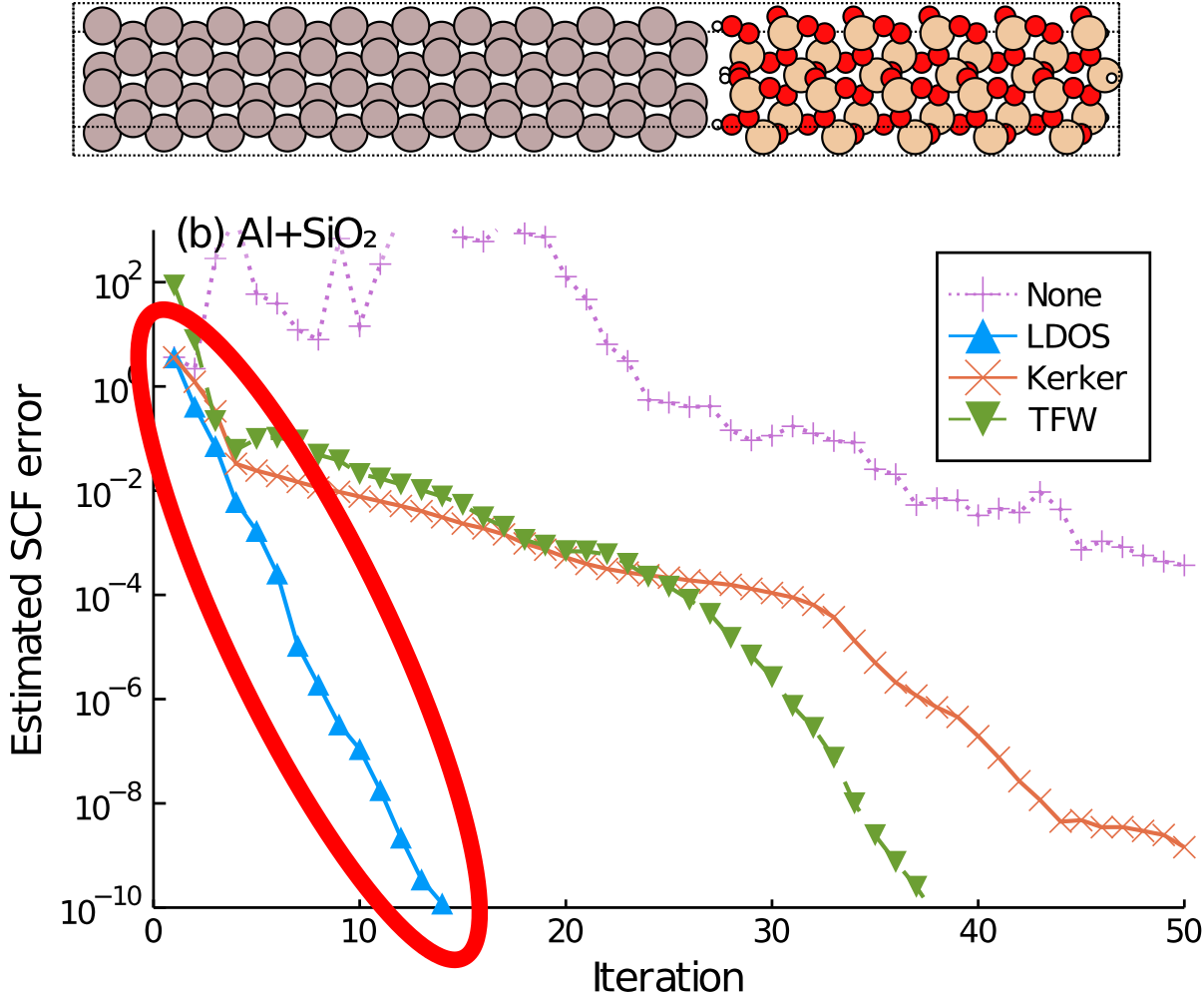Convergence of a selection of self-consistent field methods for an elongated lattice of aluminium (grey) and silica (red/yellow), shown at the top. The LDOS mixing scheme[1] (shown in blue) is able to locally adapt to the material (metal or insulator) making it converge significantly than alternatives while remaining free of any parameters.
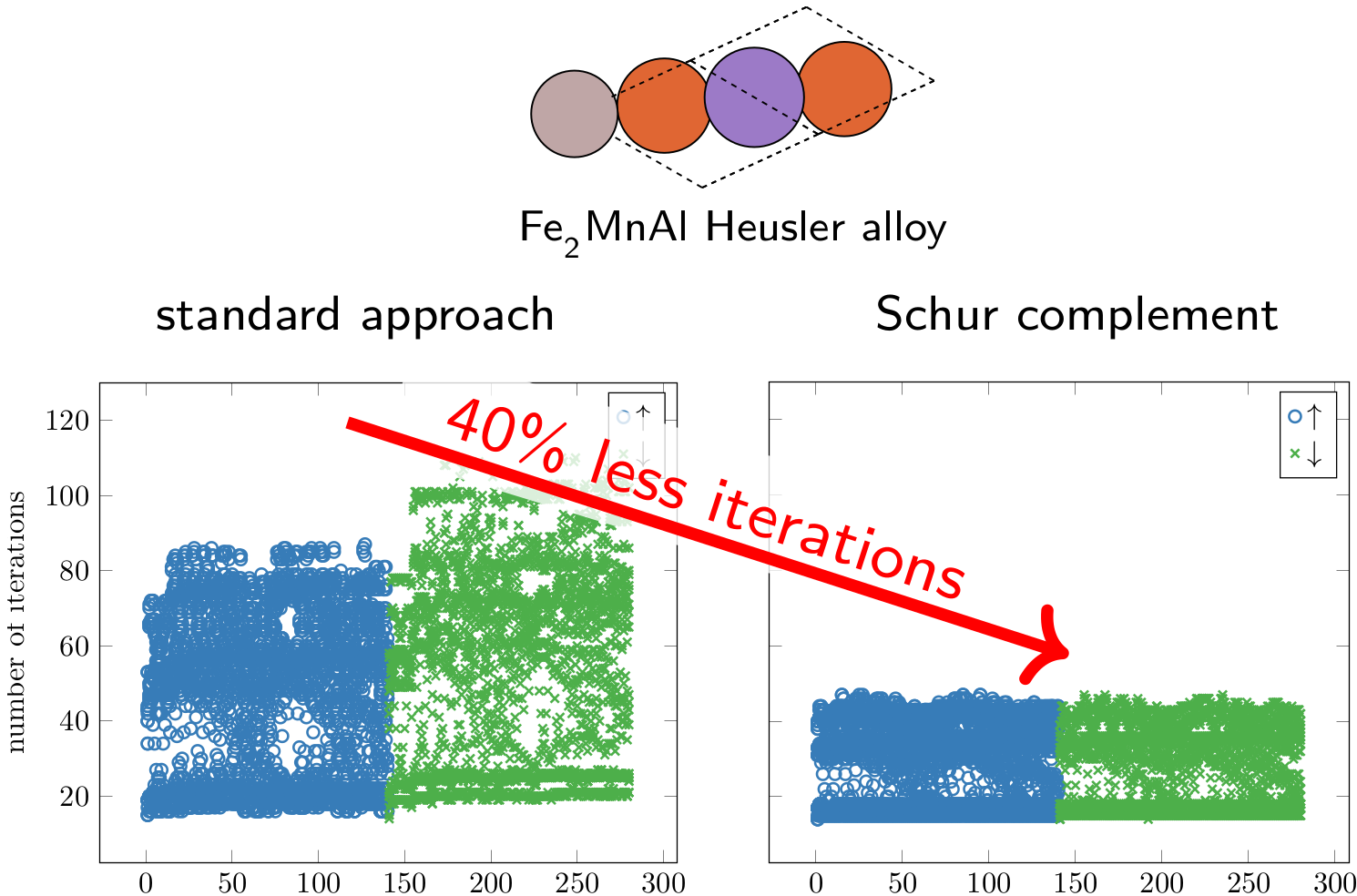Schur complement approach to response calculations[3] showing a considerable reduction in the number of iterations required to solve the Sternheimer equations in a challenging Heusler-type system.
Our current research agenda extends such ideas further. For example one question to consider is numerical stability of DFT algorithms under inexact computations. Even though standard iterative procedures (e.g. Hamiltonian diagonalisation) are usually stopped early to save computational effort, the effect of such numerical noise on the convergence of DFT algorithms has been largely neglected in the numerical analysis to date. Recently a number of opportunities to improve the efficiency of large-scale computations have emerged, which introduce further inexactness in order to increase performance. Examples are mixed-precision methods to exploit low-precision 16-bit floating-point types on modern GPU architectures. However, to safely exploit such opportunities in the DFT context, understanding and reducing the susceptibility of DFT algorithms to numerical noise is key and thus needs to be investigated more closely.
| [1] | M. F. Herbst and A. Levitt. J. Phys. Cond. Matt. 33, 085503 (2021). DOI https://doi.org/10.1088/1361-648X/abcbdb ArXiv 2009.01665 |
| [2] | M. F. Herbst and A. Levitt. J. Comp. Phys. 459, 111127 (2022). DOI https://doi.org/10.1016/j.jcp.2022.111127 ArXiv 2109.14018 |
| [3] | E. Cancès, M. F. Herbst, G. Kemlin, A. Levitt, B. Stamm. Lett. Math. Phys. 113, 21 (2023). DOI https://doi.org/10.1007/s11005-023-01645-3 ArXiv 2210.04512 |
