Due to the involved multi-scale nature of standard materials simulation workflows rigorous techniques for error estimates or uncertainty quantification (UQ) are underdeveloped and error analysis on simulation results is rarely attempted. However, recent activities to equip data-driven interatomic potentials with built-in uncertainty measures as well as recent progress on a posteriori error bounds for Kohn-Sham problems (e.g. on predicted band structures[1] or forces[2]) offer hope to achieve an error propagation all the way from the DFT level to physical observables of long-running MD trajectories.
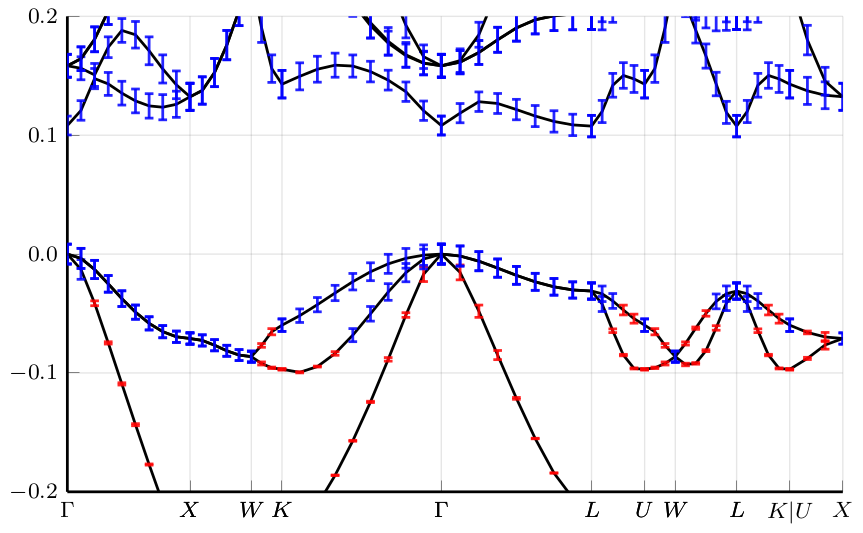Band structure of silicon in a reduced (linear) Kohn-Sham model annotated with guaranteed error bars, which indicate the total error (due to discretisation/finite basis size, early stopping of iterative procedures as well as finite floating-point arithmetic). Details in [1].
Motivated by aforementioned prospect we currently investigate both analytical as well as statistical error estimates for materials simulations in ongoing research collaborations. A key ingredient in this research is algorithmic differentiation, i.e. the ability to compute arbitrary gradients. Recently we integrated AD tools into our DFTK code (see software), making it (to the best of our knowledge) the first plane-wave DFT code, where arbitrary user-desired gradients can be computed.
Our ongoing research investigates how this ability can be exploited for sensitivity analysis, uncertainty quantification or for analytical error estimations with a first goal being to obtain a better understanding of the error of the DFT model (pseudopotential, exchange-correlation functional) in first-principle simulations.
| [1] | M. F. Herbst, A. Levitt, E. Cancès. Faraday Discuss. 224, 227 (2020). DOI https://doi.org/10.1039/D0FD00048E ArXiv 2004.13549 |
| [2] | E. Cancès, G. Dusson, G. Kemlin and A. Levitt. SIAM J. Sci. Comp. 44 (2022). DOI https://doi.org/10.1137/21M1456224 ArXiv 2111.01470 |
